Distribuciones continuas: uniforme, exponencial, y normal

Distribución Normal
http://www.ub.edu/stat/GrupsInnovacio/Statmedia/demo/Temas/Capitulo4/B0C4m1t4.htm

Fórmula:

Su función de densidad viene dada por la fórmula:

• En esta distribuciones la media coincide con el punto medio del segmento [a,b]:     

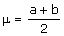
• La desviación típica es:      

Si la variable aleatoria x sigue una distribución normal con media µ y varianza

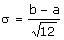
X ~ n ( µ , )

Ahora, la media proporciona una medida de posición central, mientras que la varianza da una medida de dispersión alrededor de la media.

  

El área total debajo de la curva es igual a 1. El área debajo de la curva comprendida entre µ - σ y µ + σ es aproximadamente igual a 0,68 del área total; entre µ - 2σ y µ + 2σ es aproximadamente igual a 0,95 del área total:

Es importante ver que los únicos parámetros necesarios para dibujar el gráfico de la distribución normal son la media y desviación estándar de la población. Con estos dos parámetros sabemos donde situar la campana de Gauss (En el punto correspondiente a la media) y cual es su dispersión (Determinado por la desviación estándar).

Revisar el siguiente video explicativo: 

http://www.youtube.com/watch?v=MPHcamAc5Zs&noredirect=1

Traer los apuntes del video para el martes.

Tablas del área bajo la curva: http://es.scribd.com/doc/173808664/Tabla-Normal

Ejercicio del área bajo la curva normal:

Sea X el momento elegido al azar en que una persona llega a una cita entre la 1 y las 2 de la tarde.

¿Cuál es en este caso la función de densidad?

¿Cuál es el valor medio esperado?, ¿con qué desviación típica?

Calcula la probabilidad de que llegue en la primera media hora  P(X £ 1.5)
Calcula la probabilidad de que aparezca en los últimos 15 minutos P(1.75 £ X £ 2)