Después de una prueba de laboratorio muy rigorosa con cierto componente eléctrico, el fabricante determina que en promedio, solo fallarán 2 componentes antes de tener 1 000 horas de operación. Un comprador observa que son 5 los que fallen antes de las 1 000 horas. Si el número de componentes que fallan es una variable aleatoria Poisson ¿Existe suficiente evidencia para dudar de la conclusión del fabricante?
En este caso se tiene:
Se supone que la frecuencia con que ocurren las fallas es constante e igual a dos por cada mil horas o un promedio de 1/500 unidades por hora. La probabilidad de que fallen cinco componentes en mil horas es:
La fórmula que se debe ingresar a excel es: =POISSON(x,media,acumulado), donde el acumulado es un valor lógico que determina la forma de la distribución de probabilidad devuelta. Si el argumento del acumulado es:
- FALSO: la funcón devuelve la probabilidad de Poisson de que un suceso ocurra exactamentex veces.
- VERDADERO: La función devuelve la probabilidad de Poisson de que un suceso aleatorio ocurra un número de veces comprendido entre 0 y x.
Ejercicio:
a) Supongamos que el número de accidentes laborales semanales es en promedio 3. Calcular la probabilidad de que en una semana ocurran como mínimo 2 accidentes.
b) Calcular la probabilidad de que ocurran desde 1 a 8 accidentes. Para ello elabora una tabla y gráfica. Interpreta los resultados.
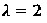

No hay comentarios:
Publicar un comentario