Objetivo: Conocer la forma de calcular las distribuciones de probabilidad para variables discretas usando Microsoft Excel para la solución de problemas prácticos.
La distribución de probabilidad binomial es uno de los modelos matemáticos que se utiliza cuando la variable aleatoria discreta es el número de éxitos en una muestra compuesta por n observaciones.
PROPIEDADES:
- La muestra se compone de un número fijo de observaciones n
- Cada
observación se clasifica en una de dos categorías,
mutuamente excluyentes (los
eventos no pueden ocurrir de manera simultánea. Ejemplo: Una
persona no puede ser de ambos sexos) y
colectivamente exhaustivos (uno de los eventos debe ocurrir. Ejemplo: Al lanzar una moneda, si no ocurre cruz, entonces ocurre cara). A estas categorías se las denomina
éxito y fracaso.
- La probabilidad de que una observación se clasifique como éxito, p, es constante de una observación o otra. De la misma forma, la probabilidad de que una observación se clasifique como fracaso, 1-p, es constante en todas las observaciones.
- La variable aleatoria binomial tiene un rango de 0 a n
Ecuación:
Donde
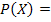
Probabilidad de X éxitos, dadas
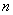
y
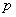
n = Número de observaciones
p = Probabilidad de éxitos
1-p = Probabilidad de fracasos
X = Número de éxitos en la muestra (
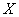
= 0, 1, 2, 3, 4,………
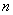
)
Ejemplos:
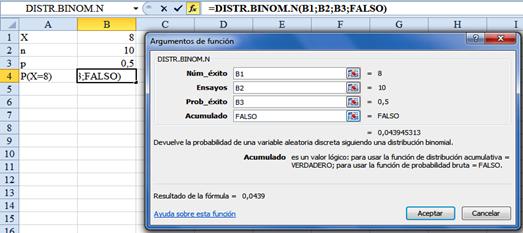
1) Determine P(X=8) para n = 10 y p = 0.5Solución:
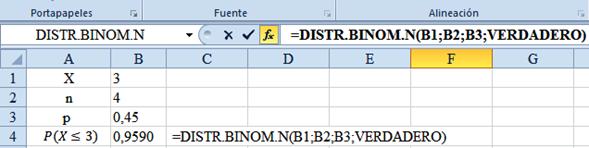
2) Determinar P(X<=3) para n =4 y p = 0.45
Ejercicios:
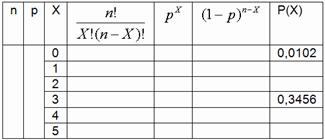
1. El 60% de profesionales leen su contrato de trabajo, incluyendo las letras pequeñas. Suponga que el número de empleados que leen cada una de las palabras de su contrato se puede modelar utilizando la distribución binomial. Considerando un grupo de cinco empleados. Llena la siguiente tabla usando Excel:
Cuál es la probabilidad de que:
a) Los cinco lean cada una de las palabras de su contrato
b) Al menos tres lean cada una de las palabras de su contrato
c) Menos de dos lean cada una de las palabras de su contrato
2) Supongamos que un jugador ante una ruleta francesa ha decidido apostarle una unidad plena al número 17 negro durante los siguientes 36 tiros de la bola en la ruleta, con la creencia de que dentro de esos 36 tiros la bola se detendrá por lo menos 3 veces en el 17 negro. Si este jugador a partir del modelo de la Distribución Binomial desea calcular cuál es la probabilidad existente para que el 17 negro aparezca 3 veces exitosas dentro de 36 tiros de la bola, deberá tener en cuenta que la probabilidad para que el 17 negro aparezca en un solo lanzamiento de la bola es de P = 1/37. Aplicar la fórmula de la Distribución Binomial para que el jugador descubra la probabilidad de que el 17 negro aparezca 3 veces dentro de 36 tiros de la bola en la ruleta francesa.
Calcular también la probabilidad de que el 17 negro aparezca 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 veces. Elabora una tabla y gráfica los datos. Interpreta los resultados obtenidos.
Leer más: http://www.monografias.com/trabajos89/ejercicios-distribucion-binomial-resueltos-excel/ejercicios-distribucion-binomial-resueltos-excel.shtml#ixzz2gLEHAE7c
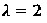

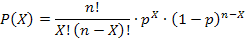
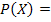 Probabilidad de X éxitos, dadas
Probabilidad de X éxitos, dadas 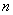 y
y 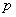
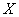 = 0, 1, 2, 3, 4,………
= 0, 1, 2, 3, 4,………